
水の運動
流速と流量
水の流れの速さ、つまり単位時間に流れる距離を流速(υ)といい、流れの方向に垂直に切った横断面積を流積(A)、単位時間内に流れる水の容積を流量(Q)といいます。
これらの間には次式の関係が成り立ちます。
Q = υ・A ⇒ υ = Q / A
流量 = 流速 x 流積 ⇒ 流速 = 流量 / 流積
単位:流速(m/s) 流積(m2) 流量(m3/s)
流体の速度は単位時間当たりの移動距離になります。この場合、方向も考えるのでベクトルとなります。速さあるいは流速の大きさを考えるときは、スカラとなります。
実際の水の流れは、水路の壁と水との間、水と水との間の摩擦力が働くため、断面の各部分の流速は異なっています。しかし、このような変化を厳密に考慮することは非常に複雑になるので、一般には取り扱いを簡単にするために上の式のように、ある断面を流れる流量を流積で割った平均の流速を考えることにします。
このような流速を平均流速といいます。とくに特記がない限りは、流速といえば平均流速のことをいいます。
流線,流跡
流体の流れを表す線に流線、流跡があります。流れの可視化によって得られた線がいずれの線であるかを知ることは重要です。
水の流れは水粒子の運動です。この水粒子の運動した経路を流跡線といいます。また、運動している水粒子は速度(ベクトルで、大きさと方向をもっている)を有しているが、ある瞬間における各水粒子の速度(ベクトル)は流れの中に無数に存在します。これらの流速の方向に接線を引いてできる曲線を流線といいます。
流線の可視化を試みるには、流れの中に小さい粒子を多数ランダムに分布させ、露出時間を短くして写真撮影をします。それぞれの粒子は短い線分として写り、これらの線分に接するような曲線を描けば流線になります。
流線はその瞬間における速度ベクトルの包絡線であるので、それぞれの点において速度ベクトルと流線の方向は一致します。
次に、ある瞬間に水の流れを横切って一つの閉じた曲線を考え、この曲線上の各点を通る流線を描くと流線で囲まれた管ができます。これを流管といいます。
粘性流体と非粘性流体
流体の粘性に着目して流体を分類すると、実在する流体は粘性の影響の大小により、以下のように分類されます。
・粘性流体 :粘性を考慮する必要がある流体
・非粘性流体:粘性を無視できる流体
物体や壁から十分に離れた所では粘性の影響は小さく、非粘性流体と近似することができます。同じ流体でも壁付近では粘性流体として扱う場合があります。
圧縮性流体と非圧縮性流体
一般に流体に作用する圧力が増大すると流体は圧縮され、その体積は減少します。このような流体の性質を圧縮性といい、液体よりも気体の方が圧縮性は著しくなります。
圧縮されやすい気体は圧縮性流体といい、これに対して圧縮されにくい液体は、一般に非圧縮性流体と呼ばれています。
理想流体と実在流体
粘性および圧縮性のない流体を理想流体といいます。理想流体では粘性がないためエネルギー損失や抵抗力が存在せず、実在する流体と矛盾する点もあります。
理想流体ではせん断応力を受けず、壁面上でも流体は流れています。一方、実在する流体では粘性の影響により壁面上で速度が0になり、壁面付近に速度の遅い境界層ができます。しかし、境界層の外側の主流領域では粘性の影響が小さく、理想流体として近似できます。境界層は通常薄い層なので、流れ場の大部分は理想流体とみなすことができ、解析が非常に容易になります。理想流体のことを完全流体とも呼びます。
定常流と非定常流
定常流とは時間によって変化しない流れのことです。人口水路の流れはこれに当たります。一方、非定常流とは時間とともに変化する流れのことで、振動流がその例としてあげられます。
振動流とは、水面の波や血液の流れのように速度と圧力が周期的に変化する流れのことです。洪水時の河川、潮の干満の影響を受ける河川の流れは非定常流に当たります。
層流と乱流
流れには層流と乱流という二つの状態があり、1880年頃レイノルズ(O.Reynolds)は、流れが層流になるか乱流になるかはレイノルズ数(Re)という無次元量によって整理されることを実験的に発見しました。
レイノルズは円管内に水を流し、その中央に着色液を注入して広がりを調べました。
流速が小さい場合、着色液はほとんど混合されず、ほぼ一本の線で流れ層流と呼ばれます。
流速が大きい場合、着色液は管全体に広がり、乱流と呼ばれます。乱流では、大小不規則な渦によって各点の速度は常に変動し、管軸に垂直な方向の速度変動も存在します。この速度変動によって、着色液の拡散が行われます。
一方、層流では速度変動はなく、流れは管軸に平行に進んでいきます。
レイノルズは、様々な条件の下で実験した結果、次のレイノルズ数(Re)によって層流と乱流を整理できることを発見しました。
Re = υd / ν
ここで、υは断面平均速度(流量/断面積)
dは管の内径
νは流体の動粘性係数
レイノルズ数(Re)は無次元量となります。
円管内の流れの場合、レイノルズ数がおよそ2300以下のとき、流れは必ず層流となり、およそ2300以上のときには、ほぼ乱流となります。
層流から乱流へと遷移を始める2300を限界レイノルズ数(Rec)といい、流路の形によってその値は異なったものとなります。
Sponsored Link
一次元流れ
一般の流れは三次元的ですが、これを一次元で考えてよい場合があります。
たとえば、管内の流れを考えるとき、平均速度で考えれば、一次元の流れとなって取り扱いが簡単になります。
下記から、流れを取り扱う上で重要な三つの基本原理、連続の式・ベルヌーイの定理・運動量の法則について説明します。連続の式は質量保存則、ベルヌーイの式はエネルギー保存則からそれぞれ導かれます。
連続の式
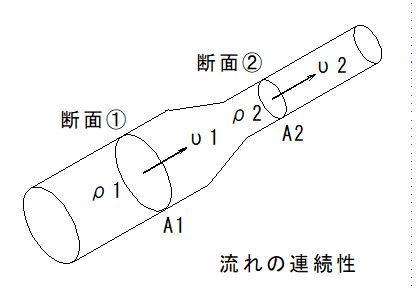
下図のように、流れを定常と仮定して、流管の一部分①~②を取り出して、その断面と流速の関係を調べてみます。
流管の管軸方向に垂直な断面①,②の断面積をA1,A2として、断面①,②における流速および密度をそれぞれυ1,υ2およびρ1,ρ2とすると、断面①からδt時間に入ってくる流体の質量はρ1・A1・υ1・δtで、断面②からδt時間に出ていく流体の質量はρ2・A2・υ2・δtになります。
流れが定流で、流体は流管を横切って出入りすることはないので、質量保存の法則から、流管①,②内の質量は常に一定でなければなりません。
したがって、単位時間に断面①から流入する質量と断面②から流出する質量とは相等しく、次式で表せます。
ρ1・A1・υ1 = ρ2・A2・υ2
ここで、断面①,②は任意の断面であるから、流管のどの部分においても成立し
ρ・A・υ = const.(一定)
となります。流体が非圧縮性とみなすことができれば、ρは一定(const.)ですから
A・υ = const. = Q(流量)
となります。ここに、Qは流量で、この関係式を連続の式といいます。
ベルヌーイの定理
静止の状態にある質点mの物体を高い所から落とすと、物体は落下運動をします。静止の状態にあった物体は位置のエネルギー(mgh)をもっており、落下運動にともなって位置のエネルギーを失いながら等量の運動エネルギー(1/2mυ2)が増します。この両者を加えるとどの場所でもエネルギーが同じになります。
これをエネルギー保存の法則といいます。
高さを持った水、速度をもった水、圧力をもった水は仕事をする能力を持っています。つまり、エネルギーを保持しています。
下図のような一つの流管を考え、二つの任意断面①,②をとり、この断面の断面積をa1,a2、流速をυ1,υ2、圧力をp1,p2、任意に取った基準面からの高さをz1,z2、水の密度をρとすると、エネルギー保存の法則から、断面①を流入するときにもっているエネルギーは、断面②を流出するときにもっているエネルギーに等しくなります。
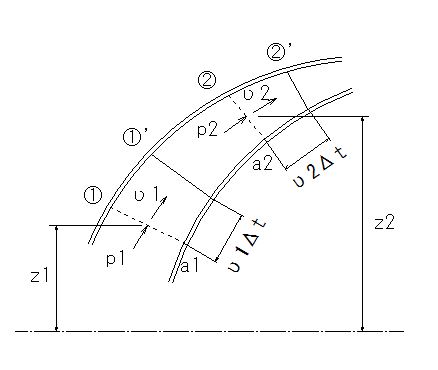
断面①,②間の水塊は水圧pによる仕事量(圧力x距離)の結果、断面①’,②’へ移動したものと考えます。
微小時間Δtの間になされた断面①および断面②でのエネルギーは次のようになります。
Δtの間に断面①に流入する水の質量
ρ・a1・υ1・Δt = ρ・Q・Δt
Δtの間に断面②から流出する水の質量
ρ・a2・υ2・Δt = ρ・Q・Δt
ここで、Qはこの流管内を流れる流量を示します。
この時、運動エネルギー,位置エネルギー,圧力のエネルギーの変化は下表のようになります。

これらの三つのエネルギーがつり合うことから次の関係が成立します。
運動エネルギーの変化量 + 位置エネルギーの変化量 = 圧力による仕事量
1/2ρQ(υ22 - υ12)Δt + ρgQ(z2 ー z1)Δt
=(p1a1υ1 - p2a2υ2)Δt
ここで、連続の式から、a1υ1 = a2υ2 = Q であり、
ρg = ω(水の単位体積重量)であるから
これを代入して上式を整理すると
υ12/2g + z1 + p1/ω = υ22/2g + z2 + p2/ω
となります。
断面①,②は任意に選んだので、上式は流管に沿ってどの断面にも成立しますから、次のように書くことができます。
υ2/2g + z + p/ω = const. = H(全水頭)
このような関係を定常流におけるベルヌーイ(Bernoulli)の定理といい、上の式をベルヌーイの式といいます。
ベルヌーイの式におけるそれぞれの項の単位は長さの単位(m)になりますから、各項とも高さで表現することができます。
ここで、υ2/2gを速度水頭、zを位置水頭、p/ωを圧力水頭と呼び、各水頭の総和Hを全水頭といいます。
運動量の法則
ホースで水を勢いよく壁に当てると、壁は水から力を受けます。また、ジェットエンジンのように、後方に勢いよく流体を吹き出すとその反作用として推進力を生じます。このときの流れと力の関係は運動量の法則によって説明できます。結局、ニュートン(Newton)の運動法則に従って、流体の運動変化量は流体に働く力に等しくなります。
質量mの物体が速度υで運動しているとき、mとυの積mυを運動量といいます。
ニュートンの運動の第二法則は
物体に作用する力(F)= 質量(m)x 加速度(α)
で表されます。
力(F)は運動量mυを用いて表すことができ、数式で表すと、
F = d(mυ)/ dt ・・・式(6-1)
となります。
この式を差分形式で表現すると
F =(m2υ2 - m1υ1)/ Δt ・・・式(6-2)
となります。
式(6-2)はm1υ1の運動量をもっている物体が移動してΔt時間後にm2υ2の運動量をもったとすると、この物体に働いた力がFであることを示しています。
式(6-1)から、「物体に作用する力は、その物体のもつ運動量の単位時間当たりの変化に等しい」といえます。これを運動量の法則といいます。
質量(m)= 密度(ρ)x 体積(V)であるので
m/Δt = ρQ
で表すことができます。
密度が一定のとき、運動量の時間変化は次式で表されます。
F = ρQ2υ2 - ρQ1υ1
流量が一定で定常流れの場合は、
F = ρQ(υ2 - υ1)
となります。
次に、流れが二次元(xおよびy方向の成分)の場合、x,y方向の流速および力の成分をそれぞれuおよびFx,υおよびFyとします。運動量の法則を、x,y方向それぞれに対して適用すると、
Fx = ρQ(u2 - u1)
Fy = ρQ(υ2 - υ1)
となります。
ニュートンの運動法則
第一法則 「外部から力を受けなければ、物体は静止するか等速運動をする」
第二法則 「物体に力が働くと加速度が生ずる。質量をm,加速度をα,
力をFとすると、F = Mα である」
第三法則 「二つの物体が直接互いに及ぼし合う力(作用と反作用)は、
同一線上で大きさが等しく向きが逆である」
Sponsored Link