
流体は自由に変形できる物質です。流体が運動している状態を「流れ」と言います。流体を特徴づけるものとして「粘性」という性質があり、水の抵抗を発生させる原因となります。
Sponsored Link
各物性値の定義
流体の特性を表す値が物性値です。水理学で特に重要な物性値の定義について説明します。
流体の密度、比重量、比重
流体の単位体積当たりの質量を密度 p といいます。質量 M の物質が体積 V のとき、その物質の密度(p)は、
p = M(質量) / V(体積)
となり、国際単位系SIで密度の単位はkg/m3を用います。
密度は状態量であり、物質、温度および圧力によって定まる値です。
標準気圧(101.3kPa)4℃の水の密度は、
pω = 1000 kg/m3
また、標準気圧(101.3kPa)、15℃における標準状態の乾燥空気の密度は
p = 1.226kg/m3 ≒ 1.2kg/m3
液体の密度pと4℃における水の密度pωの比を比重sといい、下記の式で表します。
s = p / pω
密度の逆数を比体積νといい、下記の式で表します。
ν = 1 / p
単位体積当たりの重量を比重量といい、密度に重力の加速度gが作用したものを単位体積重量ωといいます。下記の式で表します。
ω = pg
粘性係数と動粘性係数
流体の「ねばり」を表す物性値が粘度です。いい換えれば、流体を変形させるときの抵抗の大きさを代表する物性値ともいえます。
ここで下図のように、二枚の平行な平板間に流体が満たされている場合の流体の粘性について考えてみます。
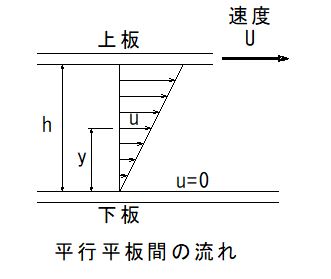
二枚の平板間の距離hは小さく、下板は固定され、上板は速度Uで移動しています。流体は固体表面に付着する性質をもっているので、上板の表面では壁面に付着して上板と同じ速度Uで右方向に移動し、下板では、速度0になります。つまり、下板からの距離yでの速度uとすると
y = 0 : u = 0
y = h : u = U
となり、これはすべりなしの条件と言われ、この式が成立するような平行流れをクエット流れといい、速度分布の形状は直線状に変化し
u = U・y / h
が成立します。
上板を速度Uで移動させるためには、力Fが必要になります。この力Fは、上板の面積Aと速度Uに比例し、距離hが小さいときには、hに反比例します。

このときの比例定数を μ とすると
F = μA・U/h
平板に作用する単位面積当たりの接線力、すなわちせん断応力τは
τ = F/A = μ・U/h = μ・u/y
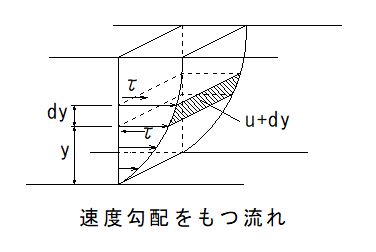
また、流れ場の速度の分布が直線状でなく、下図に示すように徐々に変化する速度分布をなしている場合には、隣接する二つの流体層の間に働くせん断応力は
τ = μ・du/dy
で表されます。
比例係数 μ を粘性係数(または粘度)といいます。
温度と圧力が一定のときには、μは一定値となります。粘性係数μの単位は、SI単位では、
μ = τy/u = (N/m2)・m/(m/s) = (N・s)/m2 =Pa・s
となります。
なお、流体の力学では、粘性係数μを密度pで除した
ν = μ/p
を用いるのが便利で、このνを動粘性係数(または動粘度)といいます。
動粘性係数νの単位は、SI単位では、
ν = μ/p = (Pa・s)/(kg/m3) = (kg・m・s)/(s2・m2)・m3/kg = m2/s
となります。
水の粘性係数および動粘性係数の値は、温度によって下表のように変化します。
| 温度[℃] | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 40 | 50 |
|---|---|---|---|---|---|---|---|---|---|
| 粘性係数μ [10-3kg/(m・s)] | 1.792 | 1.520 | 1.307 | 1.138 | 1.002 | 0.890 | 0.797 | 0.653 | 0.548 |
| 動粘性係数v [10-6m2/s] | 1.792 | 1.520 | 1.307 | 1.139 | 1.004 | 0.893 | 0.801 | 0.658 | 0.554 |
水の表面張力と毛管現象
液体は分子間引力による凝集力をもっており、液体表面では収縮しようとする力が働きます。この力を表面張力と呼び、単位長さ当たりに働く力[N/m]で表します。
水滴が草の葉で球状をしていますが、これも表面張力によって縮まろうとするからで、水滴内の圧力は大気圧より高くなります。液滴の直径をd、表面張力をT、内部の圧力上昇をΔpとすると、下図のような力のつり合いから
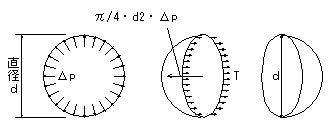
πdT = πd2/4 ・ Δp
Δp = 4T/d
と表すことができます。
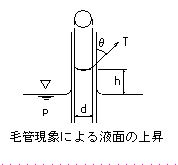
液体と固体との間には付着力が作用します。表面張力と付着力のため、液体の自由表面に細菅を立てると、下図のように管内の液面は上昇あるいは下降します。この現象を毛管現象といいます。
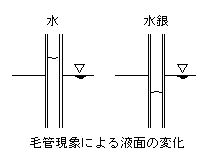
下図に示すように、管の直径をd、液体の壁に対する接触角をθ、液の密度をp、水面の平均高さをhとすると、付着力によって壁に付いた液体が表面張力によって管内の液を引き上げようとする力と管内の液体の重量とのつり合いから、次式が得られます。
πdT cosθ = pg ・ πd2/4 ・h
h = 4T cosθ / pgd
ここに、T:表面張力 p:液体の密度 g:重力の加速度
d:管の内径 pg:液体の単位重量 θ:接触角
Sponsored Link