
材料力学は、材料に働くさまざまな力によって発生する応力や変位を、公式を用いることで計算して値を求める学問です。機械設計をする上で、材料力学の知識はなくてはならない非常に大切なものです。
実際に機械設計をする過程では、材料力学の公式を暗記したり、公式の導き方を説明したりする必要はありません。また、材料力学の公式は角柱などの単純なモデルが対象ですが、実際に機械設計を行う対象は複雑な形状であるため、そのまま公式にあてはめて計算することはありません。
複雑な形状や力のかかり方を、いかに単純なモデルに置き換えて検討するかが重要になります。どういうときに、どうやって、どの公式を使うのかが、機械設計をする上で求められます。そのためには、材料力学の基本的な知識を習得し、さまざまなケースの検討を経験することが大切です。
Sponsored Link
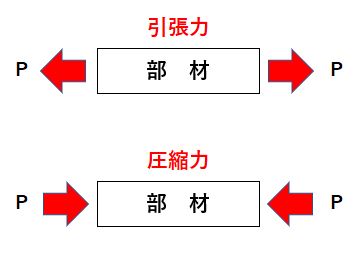
軸方向応力「軸力」
部材断面に対して、垂直の外力が作用したときの応力です。
引張力(+)と 圧縮力(-)の2種類があります。
垂直応力度 σ(シグマ)
σ = P / A
P:軸力(N)
A:断面積(mm2)
単位:N/mm2
Sponsored Link
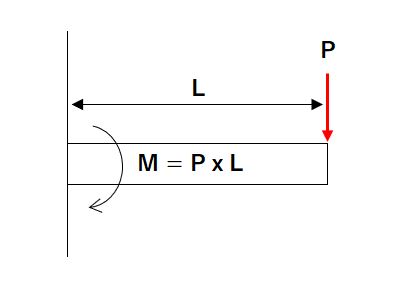
曲げモーメント(M)
曲げモーメントとは、部材を曲げる力です。
M = P ・ L
P:荷重(N)
L:距離(mm)
単位:N・mm
曲げ応力
曲げモーメントにより生じる応力です。
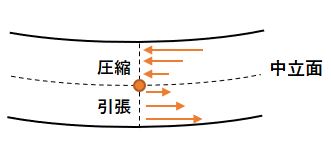
曲げの力が加わると、部材内には、引張応力と圧縮応力が発生します。
部材の中心部は、引張も圧縮も受けない中立面です。この場合、部材の下面で引張応力が最大となり、部材の上面で圧縮応力が最大となります。
曲げ応力度 σ(シグマ)
σ = M / Z
M:曲げモーメント(N・mm)
Z:断面係数(mm3)
単位:N/mm2
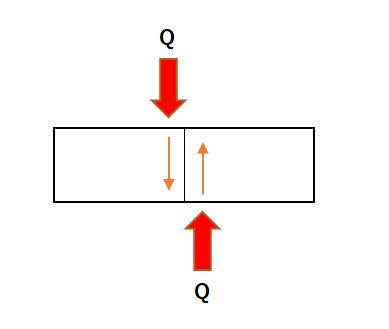
せん断力
物体内部のある面と平行方向に、その面にすべらせるように作用する応力のことです。
せん断応力度 τ(タウ)
τ = Q / A
Q:せん断力(N)
A:部材の断面積(mm2)
単位:N/mm2
補足説明
応力(N)
応力とは、外力を受けた部材内部に発生する内力のことです。応力は、部材内部に働く抵抗力であり、この抵抗力が外力と釣り合い状態にあることで部材は壊れることがなく、安全な状態を保っています。
応力度(N/mm2)
応力度とは、単位面積当たりの応力です。
よく使われるギリシャ文字はこちら
部材の断面性能はこちら
ひずみ
単位:なし
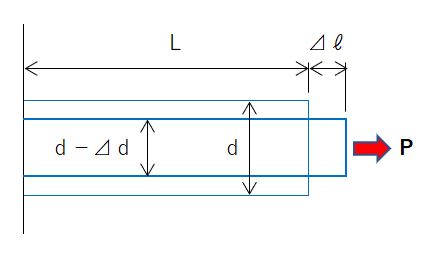
ひずみとは、物体に力が加わったときの物体の変形量と元の長さの割合をいいます。
縦ひずみ ε(イプシロン)
ε = ⊿ℓ / L
横ひずみ εh
εh = ⊿d / d
せん断ひずみ γ(ガンマ)
γ = λ / L
γ ≒ tan θ

フックの法則
変形が弾性変形の場合、垂直応力σと垂直ひずみεとの間には、次式の比例関係が成り立ちます。
σ = E ・ ε
E:ヤング率(縦弾性係数)
せん断応力τとせん断ひずみγとの間にも同様の関係が成り立ち、この場合は次式になります。
τ = G ・ γ
G:横弾性係数(せん断弾性係数)
横弾性係数Gとヤング率Eは次式のような比例関係があります。
G = E / 2(1+ν)
ν:ポアソン比
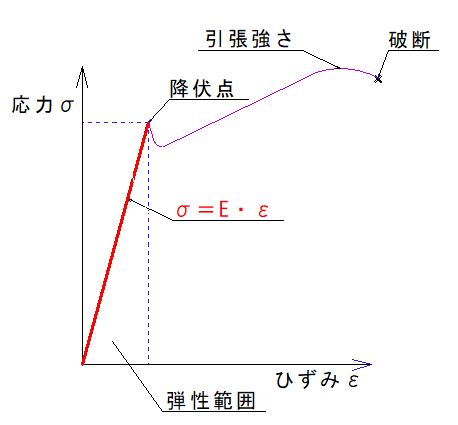
物体を引っ張ると応力σとひずみεは比例関係にあります。比例関係にある範囲を弾性範囲と言います。
弾性範囲のグラフの傾きがヤング率Eとなります。
つまり、
ヤング率の値が大きいと、変形しにくい材料
ヤング率の値が小さいと、変形しやすい材料
ということになります。
補足説明
弾性限界
弾性限界とは、応力を加えることにより生じたひずみが、除荷すれば元の寸法に戻る応力の限界値のことを言います。
ポアソン比 ν(ニュー)
縦ひずみ(ε)と横ひずみ(εh)の比率をポアソン比と言います。
ν = εh / ε
弾性限界内では材料固有の定数となり、多くの金属材料で0.3前後の値になります。
縦弾性係数(ヤング率)E と 横弾性係数G
材料固有の値で、縦弾性係数は、引張・圧縮力に対する抵抗の値。横弾性係数は、せん断力に対する抵抗の値と考えることができます。
縦弾性係数(ヤング率)と横弾性係数は比例関係にあります。
横弾性係数の値は、縦弾性係数(ヤング率)とポアソン比vから求めることができます。
G = E / 2(1+ν)
横弾性係数Gの値は、概ね縦弾性係数(ヤング率)Eの半分以下の値になります。
各鋼材のヤング率(E)
炭素鋼(SS,SM,SN,STKR等)
E=205000 N/mm2
ステンレス鋼
オーステナイト系
E=193000 N/mm2
フェライト・マルテンサイト系
E=200000 N/mm2
アルミ合金
E=69000 N/mm2
Sponsored Link
関連図書